The KU Leuven - Melbourne joint PhD program is part of an international research partnership between the University of Melbourne and the Katholieke Universiteit Leuven (KU Leuven). KU Leuven is a leading research and education university located in Leuven, Belgium. The program provides graduate researchers with an international research experience under the tutelage of world-class researchers.
Candidates participating in the joint PhD program can immerse themselves in the rich heritage of both Leuven and Melbourne, developing a global perspective and international research network. The program offers opportunities across the sciences and humanities, with projects grounded in the supervisory expertise, resources, and facilities offered by both universities.
Our partner: KU Leuven
Founded in 1425, the Katholieke Universiteit Leuven (KU Leuven) is one of the oldest universities in Europe and remains a leading research university to this day. Leuven's research is focused on nine 'key areas' that aim to tackle the societal, economic and ecological problems faced by humanity currently. Ranked by Reuters as Europe's most innovative university for the 4th year in a row, Leuven is responsible for the development of numerous life-changing innovations, such as the world's leading anti-HIV drug, Tenofovir.


2022 KU Leuven-Melbourne Research Training Group Mini Conference
The first mini conference will be held virtually on Wednesday 19 October 2022. Graduate Researchers in the Joint PhD program represent a diverse range of faculties from across the two institutions. For this conference they will deliver their research findings to-date in concise, accessible presentations. Guests are welcome.
Joint PhD Opportunity
Improving anabolic osteoporosis therapy
With ageing our bones become brittle and prone to fractures, known as osteoporosis. Despite widespread use of therapies blocking bone loss, osteoporosis still remains a major public health concern. In recent years, a new therapy - Intermittent parathyroid hormone (iPTH) – has been able to combat osteoporosis by stimulating bone formation, but suspected side effects still limit its use. This project will aim to improve bone-building therapies like iPTH by investigating the role of VEGF and PDGF signalling, two major angiogenic pathways.

The Joint PhD has given me numerous opportunities to build global networks and surround myself with world leaders in my field. Rachel Macreadie KU Leuven - Melbourne Joint PhD candidate
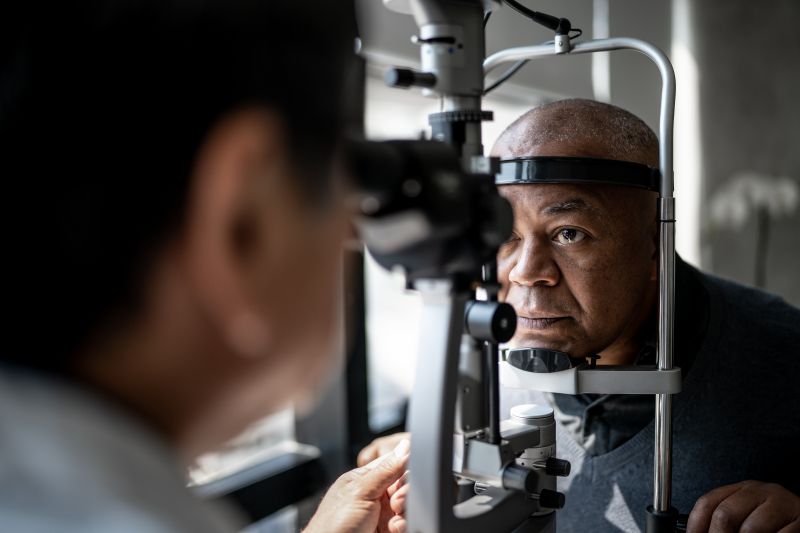
Project spotlight
Tackling neurodegenerative disorders using retinal imaging
A major clinical challenge in dementia care is the accurate and timely detection of the disease. Reliance on clinical features alone is problematic due to the overlap between dementia syndromes. Furthermore, existing tests, such as cerebrospinal fluid analysis and brain positron emission tomography (PET), are invasive, costly and not widely available. The project will seek to extend this innovation by examining whether retinal imaging can be used to detect other neuropathological processes, such as the accumulation of phosphorylated tau, alpha-synuclein or TDP-43, that contribute to dementia.
Meet our academic lead
Professor Stan Skafidas is the academic lead of the KU Leuven - Melbourne joint PhD. A faculty member of the Department of Electrical and Electronic Engineering, Professor Skafidas leads the Melbourne School of Engineering's research in nanoelectronics. An entrepreneur as well as an engineer, Professor Skafidas co-founded multiple companies including Bandspeed, a semiconductor chipset manufacturer, and Nitero, a pioneer of 60ghz technology. Both companies have since been acquired by the technology conglomerates Broadcom Inc and Advanced Micro Devices (AMD) respectively. Adaptive Frequency Hopping, a key Bluetooth technology co-invented by Professor Skafidas, continues to be used in billions of Bluetooth devices today.

First published on 26 August 2022.
Share this article
Related items
-
International PhD opportunities
Discover the fully funded Joint PhD opportunities that are currently available with universities and research institutions around the world.
-
Find a supervisor or research project
Discover how to find a supervisor and learn how they can support your graduate research, or search available research projects.
-
Research degrees
Become a graduate researcher at the University of Melbourne.
-
Your study experience
Discover what it's like to be a graduate researcher. Find out about University life, support services, and opportunities for skills development.